Pengertian Fibonacci: Deret, Rumus, Contoh Soal - Halo, adik-adik yang baik! Kali ini, kita akan membahas tentang Fibonacci. Mungkin kalian pernah mendengar tentang Fibonacci, tapi belum tahu secara detail apa itu Fibonacci dan bagaimana cara menghitung deret Fibonacci. Nah, artikel ini akan membahas semuanya dengan jelas dan mudah dipahami. Yuk, kita mulai pembahasannya!
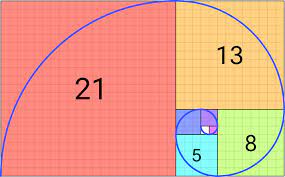 |
| Pengertian Fibonacci: Deret, Rumus, Contoh Soal |
Apa itu Fibonacci?
Fibonacci adalah nama seorang matematikawan Italia yang hidup pada abad ke-13. Nama aslinya adalah Leonardo da Pisa, tetapi ia lebih dikenal dengan nama Fibonacci. Ia dikenal karena menemukan sebuah pola bilangan yang dikenal dengan nama deret Fibonacci.
Apa itu Deret Fibonacci?
Deret Fibonacci adalah deret bilangan yang terbentuk dari penjumlahan dua bilangan sebelumnya, dimulai dari angka 0 dan 1. Jadi, deret bilangan Fibonacci dimulai dari 0, 1, kemudian hasil penjumlahan 0 + 1 = 1, hasil penjumlahan 1 + 1 = 2, hasil penjumlahan 1 + 2 = 3, dan seterusnya. Jadi, deret bilangan Fibonacci terus berlanjut dengan pola 0, 1, 1, 2, 3, 5, 8, 13, 21, dan seterusnya.
Bilangan Fibonacci
Halo, adik-adik yang baik! Kali ini, kita akan membahas tentang bilangan Fibonacci. Bilangan Fibonacci adalah salah satu jenis bilangan yang sangat menarik dan sering digunakan dalam matematika dan ilmu komputer. Nah, artikel ini akan membahas semuanya dengan jelas dan mudah dipahami. Yuk, kita mulai pembahasannya!
Bagaimana Menghitung Bilangan Fibonacci?
Untuk menghitung bilangan Fibonacci, kita dapat menggunakan rumus berikut:
F(n) = F(n-1) + F(n-2)
Di mana F(n) adalah bilangan Fibonacci ke-n, F(n-1) adalah bilangan Fibonacci sebelumnya, dan F(n-2) adalah bilangan Fibonacci sebelumnya dari F(n-1).
Contoh, jika kita ingin menghitung bilangan Fibonacci ke-10, maka langkah-langkahnya adalah sebagai berikut:
- Tentukan F(10-1) = F(9) = 34
- Tentukan F(10-2) = F(8) = 21
- Hitung F(10) = F(9) + F(8) = 34 + 21 = 55
Jadi, bilangan Fibonacci ke-10 adalah 55.
Bagaimana Menggunakan Bilangan Fibonacci dalam Ilmu Komputer?
Bilangan Fibonacci sangat berguna dalam ilmu komputer, terutama dalam bidang algoritma dan struktur data. Bilangan Fibonacci dapat digunakan, misalnya, dalam algoritma pencarian dan algoritma pengurutan. Selain itu, bilangan Fibonacci juga dapat digunakan dalam pengembangan aplikasi, seperti dalam perhitungan urutan Fibonacci untuk pengembangan game.
Rumus Deret Fibonacci
Rumus untuk menghitung angka dalam deret Fibonacci adalah sebagai berikut:
F(n) = F(n-1) + F(n-2)
Di mana F(n) adalah angka ke-n dalam deret Fibonacci, F(n-1) adalah angka sebelumnya, dan F(n-2) adalah angka sebelumnya dari F(n-1).
Contoh Soal Deret Fibonacci
Mari kita lihat contoh soal tentang deret Fibonacci. Misalnya, kita diminta untuk menentukan angka ke-10 dalam deret Fibonacci. Langkah-langkahnya adalah sebagai berikut:
- Tentukan F(10-1) = F(9) = 34
- Tentukan F(10-2) = F(8) = 21
- Hitung F(10) = F(9) + F(8) = 34 + 21 = 55
Jadi, angka ke-10 dalam deret Fibonacci adalah 55.
Bagaimana Deret Fibonacci Berguna?
Deret Fibonacci sangat berguna dalam matematika, terutama dalam bidang geometri. Deret Fibonacci dapat membantu kita dalam memahami rasio emas atau golden ratio. Rasio emas adalah perbandingan antara dua bilangan yang memiliki nilai sekitar 1,618. Rasio ini sering ditemukan dalam berbagai objek di alam, seperti spiral pada cangkang siput, spiral pada bunga matahari, dan sebagainya.
Bagaimana Menggunakan Deret Fibonacci dalam Kehidupan Sehari-hari?
Selain dalam bidang matematika dan geometri, deret Fibonacci juga dapat diterapkan dalam kehidupan sehari-hari. Misalnya, dalam dunia keuangan, deret Fibonacci dapat digunakan untuk menentukan tingkat suku bunga atau dalam merencanakan investasi. Selain itu, deret Fibonacci juga dapat digunakan dalam bidang seni, seperti dalam komposisi musik, lukisan, dan sebagainya.
Bagaimana Menghitung Deret Fibonacci dengan Cepat?
Ada beberapa cara untuk menghitung deret Fibonacci dengan cepat, salah satunya adalah dengan menggunakan rumus Binet. Rumus Binet adalah sebagai berikut:
F(n) = (phi^n - (1-phi)^n) / sqrt(5)
Di mana phi adalah rasio emas atau golden ratio, yaitu sekitar 1,618. Dalam praktiknya, rumus Binet dapat digunakan untuk menghitung deret Fibonacci yang sangat besar dengan cepat.
Bagaimana Menggunakan Deret Fibonacci dalam SEO?
Deret Fibonacci dapat digunakan dalam SEO dengan cara memanfaatkan angka dalam deret tersebut sebagai keyword. Misalnya, jika kita ingin menulis artikel tentang top 10 tips untuk meningkatkan peringkat di Google, kita dapat menggunakan angka dalam deret Fibonacci sebagai acuan untuk membuat judul artikel, misalnya "10 Tips Terbaik untuk Meningkatkan Peringkat di Google". Penggunaan angka dalam judul artikel dapat meningkatkan daya tarik bagi pembaca dan membantu meningkatkan peringkat artikel di mesin pencari Google.
Golden Ratio dan Bilangan Fibonacci
Halo, adik-adik yang baik! Kali ini, kita akan membahas tentang golden ratio dan hubungannya dengan bilangan Fibonacci. Golden ratio adalah salah satu konsep matematika yang sangat menarik, dan bilangan Fibonacci adalah salah satu bilangan yang digunakan dalam menghitung rasio emas tersebut. Nah, artikel ini akan membahas semuanya dengan jelas dan mudah dipahami. Yuk, kita mulai pembahasannya!
Apa itu Golden Ratio?
Golden ratio atau rasio emas adalah suatu proporsi atau perbandingan antara dua ukuran yang dianggap paling harmonis dan estetis, yaitu sekitar 1,618. Konsep ini telah digunakan sejak zaman kuno dalam seni, arsitektur, dan matematika.
Bagaimana Hubungan Golden Ratio dengan Bilangan Fibonacci?
Hubungan antara golden ratio dan bilangan Fibonacci adalah bahwa rasio antara dua bilangan berturut-turut dalam deret Fibonacci akan semakin mendekati rasio emas atau golden ratio ketika bilangan-bilangan tersebut semakin besar.
Contohnya, jika kita membagi bilangan Fibonacci ke-13 dengan bilangan Fibonacci ke-12, maka hasilnya akan mendekati rasio emas atau golden ratio, yaitu sekitar 1,618.
Bagaimana Menghitung Golden Ratio dengan Bilangan Fibonacci?
Untuk menghitung golden ratio dengan bilangan Fibonacci, kita dapat menggunakan rumus berikut:
phi = (1 + sqrt(5)) / 2
Di mana phi adalah rasio emas atau golden ratio, dan sqrt(5) adalah akar lima.
Kita juga dapat menggunakan bilangan Fibonacci untuk menghitung golden ratio dengan rumus berikut:
phi = F(n) / F(n-1)
Di mana F(n) dan F(n-1) adalah bilangan Fibonacci ke-n dan ke-(n-1).
Contoh Soal Fibonacci
Tentu saja, berikut adalah tiga contoh soal Fibonacci beserta jawaban yang jelas dan mudah dimengerti:
Contoh Soal 1
Hitunglah bilangan Fibonacci ke-8!
Jawaban
Bilangan Fibonacci ke-8 dapat dihitung dengan menggunakan rumus:
F(n) = F(n-1) + F(n-2)
Di mana F(8) adalah bilangan Fibonacci ke-8, F(7) adalah bilangan Fibonacci ke-7, dan F(6) adalah bilangan Fibonacci ke-6.
Maka, dapat dihitung sebagai berikut:
F(6) = 8
F(7) = 13
F(8) = F(7) + F(6) = 13 + 8 = 21
Jadi, bilangan Fibonacci ke-8 adalah 21.
Contoh Soal 2
Hitunglah rasio antara bilangan Fibonacci ke-10 dan bilangan Fibonacci ke-9, dan tentukan apakah hasilnya mendekati rasio emas atau tidak!
Jawaban
Rasio antara bilangan Fibonacci ke-10 dan bilangan Fibonacci ke-9 dapat dihitung dengan menggunakan rumus:
phi = F(n) / F(n-1)
Di mana F(10) adalah bilangan Fibonacci ke-10 dan F(9) adalah bilangan Fibonacci ke-9.
Maka, dapat dihitung sebagai berikut:
phi = F(10) / F(9) = 55 / 34 = 1.6176
Kita dapat melihat bahwa hasilnya mendekati rasio emas atau golden ratio, yang sekitar 1,618. Jadi, dapat disimpulkan bahwa rasio antara bilangan Fibonacci ke-10 dan bilangan Fibonacci ke-9 mendekati rasio emas.
Contoh Soal 3
Hitunglah jumlah dari bilangan Fibonacci ke-1 hingga bilangan Fibonacci ke-6!
Jawaban
Untuk menghitung jumlah dari bilangan Fibonacci ke-1 hingga bilangan Fibonacci ke-6, kita dapat menggunakan rumus berikut:
sum = F(n+2) - 1
Di mana F(n+2) adalah bilangan Fibonacci ke-(n+2) dan sum adalah jumlah dari bilangan Fibonacci ke-1 hingga bilangan Fibonacci ke-n.
Maka, dapat dihitung sebagai berikut:
F(8) = 21
sum = F(8+2) - 1 = F(10) - 1 = 55 - 1 = 54
Jadi, jumlah dari bilangan Fibonacci ke-1 hingga bilangan Fibonacci ke-6 adalah 54.
Kesimpulan
Deret Fibonacci adalah deret bilangan yang terbentuk dari penjumlahan dua bilangan sebelumnya, dimulai dari angka 0 dan 1. Deret Fibonacci sangat berguna dalam matematika dan membantu kita memahami rasio emas atau golden ratio. Selain itu, deret Fibonacci juga dapat diterapkan dalam kehidupan sehari-hari, seperti dalam dunia keuangan dan seni. Dalam SEO, deret Fibonacci dapat digunakan untuk membuat judul artikel yang menarik bagi pembaca dan meningkatkan peringkat artikel di mesin pencari Google. Semoga artikel ini bermanfaat bagi kalian.
FAQ
Apa itu rumus Binet?
Rumus Binet adalah rumus untuk menghitung angka dalam deret Fibonacci dengan cepat.Bagaimana cara menghitung deret Fibonacci dengan cepat?
Salah satu cara menghitung deret Fibonacci dengan cepat adalah dengan menggunakan rumus Binet.Apa manfaat menggunakan deret Fibonacci dalam SEO?
Penggunaan angka dalam deret Fibonacci dapat meningkatkan daya tarik bagi pembaca dan membantu meningkatkan peringkat artikel di mesin pencari Google.Apa kegunaan deret Fibonacci dalam seni?
Deret Fibonacci dapat diterapkan dalam bidang seni, seperti dalam komposisi musik, lukisan, dan sebagainya.Apa kegunaan deret Fibonacci dalam dunia keuangan?
Deret Fibonacci dapat digunakan dalam dunia keuangan untuk menentukan tingkat suku bunga atau dalam merencanakan investasi.


Post a Comment