Pengertian Identitas Trigonometri: Grafik, Tabel, Contoh Soal - Hello adik-adik yang baik, bertemu lagi dengan Bospedia! Pada kesempatan kali ini, kita akan membahas tentang identitas trigonometri. Apa itu identitas trigonometri? Bagaimana grafik dan tabel identitas trigonometri? Bagaimana penerapan identitas trigonometri dalam contoh soal? Semua pertanyaan ini akan dijawab dalam artikel ini dengan penjelasan yang lengkap dan mudah dipahami.
Trigonometri adalah cabang matematika yang mempelajari hubungan antara sudut dan sisi segitiga. Identitas trigonometri adalah persamaan matematika yang menunjukkan hubungan antara fungsi trigonometri. Terdapat beberapa identitas trigonometri yang penting untuk dipahami, seperti identitas Pythagoras, identitas sudut ganda, identitas sudut rangkap, dan identitas sudut setengah. Identitas trigonometri juga sering digunakan dalam perhitungan matematika, fisika, dan teknik.
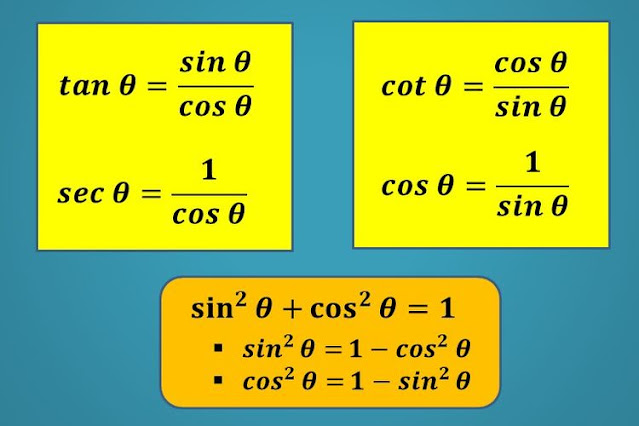 |
| Pengertian Identitas Trigonometri: Grafik, Tabel, Contoh Soal |
Grafik identitas trigonometri adalah grafik yang menunjukkan nilai fungsi trigonometri pada setiap sudut di dalam lingkaran satuan. Lingkaran satuan adalah lingkaran dengan jari-jari satu yang digunakan untuk memvisualisasikan hubungan antara sudut dan sisi segitiga. Pada grafik identitas trigonometri, garis horizontal dan vertikal digambar pada sudut-sudut tertentu untuk menunjukkan nilai fungsi trigonometri. Grafik identitas trigonometri sangat berguna untuk memahami hubungan antara fungsi trigonometri dan sudut.
Tabel identitas trigonometri adalah tabel yang berisi nilai-nilai fungsi trigonometri pada sudut-sudut tertentu. Terdapat dua jenis tabel identitas trigonometri, yaitu tabel sudut istimewa dan tabel sudut umum. Tabel sudut istimewa berisi nilai-nilai fungsi trigonometri pada sudut-sudut tertentu yang memiliki nilai sudut yang mudah diingat, seperti 0°, 30°, 45°, 60°, dan 90°. Sedangkan tabel sudut umum berisi nilai-nilai fungsi trigonometri pada sudut-sudut yang tidak termasuk sudut-sudut istimewa.
Selain itu, identitas trigonometri juga digunakan dalam perhitungan trigonometri. Contoh soal tentang identitas trigonometri seringkali melibatkan persamaan trigonometri yang harus diselesaikan menggunakan identitas trigonometri. Misalnya, jika terdapat persamaan trigonometri sin²x + cos²x = 1, identitas Pythagoras dapat digunakan untuk menyelesaikan persamaan tersebut menjadi 1 = 1.
Berikut adalah daftar isi dari artikel ini:
- Definisi Identitas Trigonometri
- Grafik Identitas Trigonometri
- Tabel Identitas Trigonometri
- Identitas Pythagoras
- Identitas Sudut Ganda
- Identitas Sudut Rangkap
- Identitas Sudut Setengah
- Penerapan Identitas Trigonometri dalam Contoh Soal
- Kesimpulan
1. Definisi Identitas Trigonometri
Identitas trigonometri adalah persamaan matematika yang menunjukkan hubungan antara fungsi trigonometri. Terdapat beberapa identitas trigonometri yang penting untuk dipahami, seperti identitas Pythagoras, identitas sudut ganda, identitas sudut rangkap, dan identitas sudut setengah.
Identitas Pythagoras adalah identitas trigonometri yang menghubungkan fungsi sinus, kosinus, dan tangen dengan menggunakan persamaan Pythagoras. Identitas Pythagoras dinyatakan dalam persamaan sin²x + cos²x = 1. Persamaan ini menunjukkan bahwa jumlah kuadrat dari fungsi sinus dan kosinus pada suatu sudut tertentu selalu sama dengan satu.
Identitas sudut ganda adalah identitas trigonometri yang menghubungkan fungsi trigonometri pada sudut ganda dengan fungsi trigonometri pada sudut asli. Identitas sudut ganda adalah dinyatakan dalam persamaan berikut:
sin 2x = 2 sin x cos x
cos 2x = cos²x - sin²x
tan 2x = 2 tan x / (1 - tan²x)
Persamaan ini sangat berguna dalam perhitungan trigonometri pada sudut ganda.
Identitas sudut rangkap adalah identitas trigonometri yang menghubungkan fungsi trigonometri pada sudut yang merupakan jumlah atau selisih dari dua sudut. Terdapat empat identitas sudut rangkap, yaitu:
sin (α + β) = sin α cos β + cos α sin β
cos (α + β) = cos α cos β - sin α sin β
sin (α - β) = sin α cos β - cos α sin β
cos (α - β) = cos α cos β + sin α sin β
Identitas sudut setengah adalah identitas trigonometri yang menghubungkan fungsi trigonometri pada sudut setengah dengan fungsi trigonometri pada sudut asli. Terdapat dua identitas sudut setengah, yaitu:
sin (x/2) = ±√[(1-cos x)/2]
cos (x/2) = ±√[(1+cos x)/2]
Identitas trigonometri sangat berguna dalam perhitungan trigonometri pada berbagai bidang, seperti matematika, fisika, dan teknik. Selanjutnya, kita akan membahas grafik dan tabel identitas trigonometri.
Grafik fungsi trigonometri
Grafik fungsi trigonometri adalah grafik yang menunjukkan nilai fungsi trigonometri pada setiap sudut di dalam lingkaran satuan. Lingkaran satuan adalah lingkaran dengan jari-jari satu yang digunakan untuk memvisualisasikan hubungan antara sudut dan sisi segitiga. Pada grafik fungsi trigonometri, sumbu x menunjukkan sudut dalam satuan derajat atau radian, sedangkan sumbu y menunjukkan nilai fungsi trigonometri.
Berikut ini adalah grafik fungsi trigonometri untuk fungsi sinus, kosinus, dan tangen:
Grafik Fungsi Sinus
Grafik fungsi sinus menunjukkan nilai sin(x) pada setiap sudut dalam lingkaran satuan. Grafik fungsi sinus memiliki bentuk gelombang yang bergentayangan antara -1 dan 1 pada setiap periode. Periode dari grafik fungsi sinus adalah 360° atau 2π radian.
Grafik Fungsi Cosinus
Grafik fungsi kosinus menunjukkan nilai cos(x) pada setiap sudut dalam lingkaran satuan. Grafik fungsi kosinus memiliki bentuk gelombang yang bergentayangan antara -1 dan 1 pada setiap periode. Periode dari grafik fungsi kosinus adalah 360° atau 2π radian.
Grafik Fungsi Tangen
Grafik fungsi tangen menunjukkan nilai tan(x) pada setiap sudut dalam lingkaran satuan. Grafik fungsi tangen memiliki bentuk yang berupa garis yang melewati titik-titik singularitas pada setiap periode. Periode dari grafik fungsi tangen adalah 180° atau π radian.
Grafik Identitas Trigonometri
Grafik identitas trigonometri adalah grafik yang menunjukkan nilai fungsi trigonometri pada setiap sudut di dalam lingkaran satuan. Lingkaran satuan adalah lingkaran dengan jari-jari satu yang digunakan untuk memvisualisasikan hubungan antara sudut dan sisi segitiga. Pada grafik identitas trigonometri, garis horizontal dan vertikal digambar pada sudut-sudut tertentu untuk menunjukkan nilai fungsi trigonometri.
Grafik identitas trigonometri sangat berguna untuk memahami hubungan antara fungsi trigonometri dan sudut. Grafik identitas trigonometri dapat digunakan untuk menentukan nilai fungsi trigonometri pada sudut tertentu. Selain itu, grafik identitas trigonometri juga dapat digunakan untuk memvisualisasikan hubungan antara fungsi trigonometri dan sudut.
Sudut Istimewa
Sudut istimewa adalah sudut yang memiliki nilai sudut yang mudah diingat dan sering digunakan dalam perhitungan trigonometri. Terdapat lima sudut istimewa yang sering digunakan dalam perhitungan trigonometri, yaitu 0°, 30°, 45°, 60°, dan 90°.
Berikut ini adalah nilai-nilai sudut istimewa dalam derajat dan radian:
- 0° = 0 rad
- 30° = π/6 rad
- 45° = π/4 rad
- 60° = π/3 rad
- 90° = π/2 rad
Sudut istimewa sangat berguna dalam perhitungan trigonometri karena nilai-nilainya dapat diingat dengan mudah dan sering muncul dalam perhitungan trigonometri pada berbagai bidang, seperti matematika, fisika, dan teknik.
Dengan menggunakan sudut istimewa, kita dapat menentukan nilai fungsi trigonometri pada sudut-sudut tertentu dengan mudah. Selain itu, sudut istimewa juga dapat digunakan untuk memudahkan perhitungan segitiga dalam berbagai bidang, seperti geometri, trigonometri, dan fisika.
Berikut ini adalah nilai-nilai fungsi trigonometri pada sudut istimewa:
| Sudut | Sinus | Kosinus | Tangen | Kotangen |
|---|---|---|---|---|
| 0° | 0 | 1 | 0 | Tak Terdefinisi |
| 30° | 1/2 | √3/2 | √3/3 | √3 |
| 45° | √2/2 | √2/2 | 1 | 1 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 |
| 90° | 1 | 0 | Tak Terdefinisi | 0 |
Sudut istimewa adalah sudut yang memiliki nilai sudut yang mudah diingat dan sering digunakan dalam perhitungan trigonometri. Terdapat lima sudut istimewa yang sering digunakan dalam perhitungan trigonometri, yaitu 0°, 30°, 45°, 60°, dan 90°. Sudut istimewa sangat berguna dalam perhitungan trigonometri karena nilai-nilainya dapat diingat dengan mudah dan sering muncul dalam perhitungan trigonometri pada berbagai bidang, seperti matematika, fisika, dan teknik.
Tabel Identitas Trigonometri
Tabel identitas trigonometri adalah tabel yang berisi nilai-nilai fungsi trigonometri pada sudut-sudut tertentu. Terdapat dua jenis tabel identitas trigonometri, yaitu tabel sudut istimewa dan tabel sudut umum.
Tabel sudut istimewa berisi nilai-nilai fungsi trigonometri pada sudut-sudut tertentu yang memiliki nilai sudut yang mudah diingat, seperti 0°, 30°, 45°, 60°, dan 90°. Sedangkan tabel sudut umum berisi nilai-nilai fungsi trigonometri pada sudut-sudut yang tidak termasuk sudut-sudut istimewa.
Tabel identitas trigonometri sangat berguna dalam perhitungan trigonometri pada berbagai bidang, seperti matematika, fisika, dan teknik. Selain itu, tabel identitas trigonometri juga dapat digunakan untuk memudahkan perhitungan trigonometri pada sudut tertentu.
Identitas Pythagoras
Identitas Pythagoras adalah identitas trigonometri yang menghubungkan fungsi sinus, kosinus, dan tangen dengan menggunakan persamaan Pythagoras. Identitas Pythagoras dinyatakan dalam persamaan sin²x + cos²x = 1. Persamaan ini menunjukkan bahwa jumlah kuadrat dari fungsi sinus dan kosinus pada suatu sudut tertentu selalu sama dengan satu.
Identitas Pythagoras sangat berguna dalam perhitungan trigonometri pada berbagai bidang, seperti matematika, fisika, dan teknik. Selain itu, identitas Pythagoras juga dapat digunakan untuk menyelesaikan persamaan trigonometri yang lebih kompleks.
Identitas Sudut Ganda
Identitas sudut ganda adalah identitas trigonometri yang menghubungkan fungsi trigonometri pada sudut ganda dengan fungsi trigonometri pada sudut asli. Terdapat tiga persamaan identitas sudut ganda, yaitu:
sin 2x = 2 sin x cos x
cos 2x = cos²x - sin²x
tan 2x = 2 tan x / (1 - tan²x)
Persamaan ini sangat berguna dalam perhitungan trigonometri pada sudut ganda. Dengan menggunakan identitas sudut ganda, kita dapat menghitung nilai fungsi trigonometri pada sudut ganda dengan mudah.
Identitas Sudut Rangkap
Identitas sudut rangkap adalah identitas trigonometri yang menghubungkan fungsi trigonometri pada sudut yang merupakan jumlah atau selisih dari dua sudut. Terdapat empat persamaan identitas sudut rangkap, yaitu:
sin (α + β) = sin α cos β + cos α sin β
cos (α + β) = cos α cos β - sin α sin β
sin (α - β) = sin α cos β - cos α sin β
cos (α - β) = cos α cos β + sin α sin β
Persamaan ini sangat berguna dalam perhitungan trigonometri pada sudut rangkap. Dengan menggunakan identitas sudut rangkap, kita dapat menghitung nilai fungsi trigonometri pada sudut yang merupakan jumlah atau selisih dari dua sudut dengan mudah.
Identitas Sudut Setengah
Identitas sudut setengah adalah identitas trigonometri yang menghubungkan fungsi trigonometri pada sudut setengah dengan fungsi trigonometri pada sudut asli. Terdapat dua persamaan identitas sudut setengah, yaitu:
sin (x/2) = ±√[(1-cos x)/2]
cos (x/2) = ±√[(1+cos x)/2]
Persamaan ini sangat berguna dalam perhitungan trigonometri pada sudut setengah. Dengan menggunakan identitas sudut setengah, kita dapat menghitung nilai fungsi trigonometri pada sudut setengah dengan mudah.
Persamaan Trigonometri
Persamaan trigonometri adalah persamaan yang mengandung fungsi-fungsi trigonometri, seperti sin(x), cos(x), dan tan(x). Persamaan trigonometri dapat diselesaikan dengan menggunakan identitas trigonometri dan sifat-sifat fungsi trigonometri.
Setiap fungsi trigonometri memiliki nilai yang berbeda pada setiap kuadran pada lingkaran satuan. Oleh karena itu, persamaan trigonometri dapat memiliki solusi yang berbeda pada setiap kuadran. Berikut ini adalah persamaan trigonometri pada setiap kuadran pada lingkaran satuan:
Persamaan Trigonometri di Kuadran I
Kuadran I adalah kuadran yang terletak di atas sumbu x positif. Pada kuadran I, nilai sin(x), cos(x), dan tan(x) selalu positif. Oleh karena itu, persamaan trigonometri pada kuadran I dapat diselesaikan dengan menggunakan nilai-nilai positif dari fungsi trigonometri.
Contoh persamaan trigonometri pada kuadran I: sin(x) = 1/2
Solusi: x = 30° atau x = π/6 radian
Persamaan Trigonometri di Kuadran II
Kuadran II adalah kuadran yang terletak di atas sumbu x negatif. Pada kuadran II, nilai sin(x) positif, tetapi nilai cos(x) negatif. Oleh karena itu, persamaan trigonometri pada kuadran II dapat diselesaikan dengan menggunakan identitas sudut rangkap sin(180° - x) = sin(x) dan cos(180° - x) = -cos(x).
Contoh persamaan trigonometri pada kuadran II: cos(x) = -1/2
Solusi: x = 120° atau x = 2π/3 radian
Persamaan Trigonometri di Kuadran III
Kuadran III adalah kuadran yang terletak di bawah sumbu x negatif. Pada kuadran III, nilai sin(x) dan cos(x) selalu negatif, sedangkan nilai tan(x) positif. Oleh karena itu, persamaan trigonometri pada kuadran III dapat diselesaikan dengan mengubah tanda dari nilai sin(x) dan cos(x) menjadi positif dan menggunakan identitas sudut rangkap sin(x + 180°) = -sin(x) dan cos(x + 180°) = -cos(x).
Contoh persamaan trigonometri pada kuadran III: tan(x) = 2
Solusi: x = 63.43° atau x = 2.1588 radian
Persamaan Trigonometri di Kuadran IV
Kuadran IV adalah kuadran yang terletak di bawah sumbu x positif. Pada kuadran IV, nilai sin(x) negatif, tetapi nilai cos(x) positif. Oleh karena itu, persamaan trigonometri pada kuadran IV dapat diselesaikan dengan mengubah tanda dari nilai sin(x) menjadi positif dan menggunakan identitas sudut rangkap sin(360° - x) = -sin(x) dan cos(360° - x) = cos(x).
Contoh persamaan trigonometri pada kuadran IV: cos(x) = 3/4
Solusi: x = 41.41° atau x = 0.7227 radian
Persamaan trigonometri adalah persamaan yang mengandung fungsi-fungsi trigonometri, seperti sin(x), cos(x), dan tan(x). Persamaan trigonometri dapat diselesaikan dengan menggunakan identitas trigonometri dan sifat-sifat fungsi trigonometri. Setiap fungsi trigonometri memiliki nilai yang berbeda pada setiap kuadran pada lingkaran satuan. Oleh karena itu, persamaan trigonometri dapat memiliki solusi yang berbeda pada setiap kuadran.
Identitas Trigonometri
Identitas trigonometri adalah persamaan matematika yang menghubungkan fungsi trigonometri pada sudut-sudut tertentu. Terdapat banyak identitas trigonometri yang dapat digunakan untuk menyederhanakan atau menyelesaikan persamaan trigonometri. Identitas trigonometri dapat dikelompokkan menjadi tiga kategori berdasarkan fungsi trigonometri yang terlibat, yaitu identitas trigonometri terhadap sinus, cosinus, dan tangen.
Berikut ini adalah identitas trigonometri terhadap sinus, cosinus, dan tangen:
Identitas Trigonometri Terhadap Sinus
- Sin(-x) = -sin(x)
- Sin(x + y) = sin(x) cos(y) + cos(x) sin(y)
- Sin(x - y) = sin(x) cos(y) - cos(x) sin(y)
- Sin(2x) = 2 sin(x) cos(x)
- Sin(3x) = 3 sin(x) - 4 sin^3(x)
- Sin(4x) = 4 sin(x) cos(x) - 8 sin^3(x) cos(x)
Identitas Trigonometri Terhadap Cosinus
- Cos(-x) = cos(x)
- Cos(x + y) = cos(x) cos(y) - sin(x) sin(y)
- Cos(x - y) = cos(x) cos(y) + sin(x) sin(y)
- Cos(2x) = cos^2(x) - sin^2(x) = 2 cos^2(x) - 1 = 1 - 2 sin^2(x)
- Cos(3x) = 4 cos^3(x) - 3 cos(x)
- Cos(4x) = 8 cos^4(x) - 8 cos^2(x) + 1
Identitas Trigonometri Terhadap Tangen
- Tan(-x) = -tan(x)
- Tan(x + y) = (tan(x) + tan(y)) / (1 - tan(x) tan(y))
- Tan(x - y) = (tan(x) - tan(y)) / (1 + tan(x) tan(y))
- Tan(2x) = (2 tan(x)) / (1 - tan^2(x))
Identitas trigonometri adalah persamaan matematika yang menghubungkan fungsi trigonometri pada sudut-sudut tertentu. Terdapat banyak identitas trigonometri yang dapat digunakan untuk menyederhanakan atau menyelesaikan persamaan trigonometri. Identitas trigonometri dapat dikelompokkan menjadi tiga kategori berdasarkan fungsi trigonometri yang terlibat, yaitu identitas trigonometri terhadap sinus, cosinus, dan tangen.
Penerapan Identitas Trigonometri dalam Contoh Soal
Identitas trigonometri seringkali digunakan dalam perhitungan trigonometri pada berbagai bidang, seperti matematika, fisika, dan teknik. Contoh soal tentang identitas trigonometri seringkali melibatkan persamaan trigonometri yang harus diselesaikan menggunakan identitas trigonometri.
Soal Identitas Trigonometri
Berikut ini adalah tiga contoh soal identitas trigonometri beserta pembahasannya:
1. Bukti bahwa identitas trigonometri sin^2(x) + cos^2(x) = 1 benar untuk setiap nilai x.
Pembahasan:
Kita dapat menggunakan identitas pythagoras pada segitiga siku-siku dengan sudut x sebagai sudut lancip. Dalam segitiga tersebut, sin(x) = a/c dan cos(x) = b/c. Oleh karena itu, sin^2(x) + cos^2(x) = (a/c)^2 + (b/c)^2 = (a^2 + b^2)/c^2 = 1, karena a^2 + b^2 = c^2 berdasarkan identitas pythagoras. Oleh karena itu, identitas trigonometri sin^2(x) + cos^2(x) = 1 benar untuk setiap nilai x.
2. Bukti bahwa identitas trigonometri 1 + tan^2(x) = sec^2(x) benar untuk setiap nilai x.
Pembahasan:
Kita dapat menggunakan identitas trigonometri cos^2(x) + sin^2(x) = 1 dan membagi kedua sisi dengan cos^2(x). Dengan demikian, kita dapat menghasilkan identitas trigonometri yang mengandung tan(x) dan sec(x). Secara khusus, kita dapat menghasilkan 1 + tan^2(x) / cos^2(x) = 1 / cos^2(x), yang dapat disederhanakan menjadi 1 + tan^2(x) = sec^2(x) berdasarkan definisi sec(x) = 1/cos(x). Oleh karena itu, identitas trigonometri 1 + tan^2(x) = sec^2(x) benar untuk setiap nilai x.
3. Bukti bahwa identitas trigonometri sin(x) cos(x) = (1/2) sin(2x) benar untuk setiap nilai x.
Pembahasan:
Kita dapat menggunakan identitas trigonometri sin(2x) = 2 sin(x) cos(x) dan membagi kedua sisi dengan 2. Dengan demikian, kita dapat menghasilkan identitas trigonometri yang mengandung sin(x) dan cos(x) dalam bentuk sin(2x) / 2 = sin(x) cos(x). Oleh karena itu, identitas trigonometri sin(x) cos(x) = (1/2) sin(2x) benar untuk setiap nilai x.
Kesimpulan
Identitas trigonometri adalah persamaan yang menghubungkan fungsi trigonometri pada sudut-sudut tertentu. Terdapat beberapa jenis identitas trigonometri, seperti identitas Pythagoras, identitas sudut ganda, identitas sudut rangkap, dan identitas sudut setengah. Identitas trigonometri sangat berguna dalam perhitungan trigonometri pada berbagai bidang, seperti matematika, fisika, dan teknik. Selain itu, grafik dan tabel identitas trigonometri juga dapat digunakan untuk memudahkan perhitungan trigonometri pada sudut tertentu.


Post a Comment