Pengertian Nilai Mutlak: Persamaan, Pertidaksamaan & Contoh Soal - Hello adik-adik yang baik, bertemu lagi dengan Bospedia! Kali ini, kita akan membahas tentang nilai mutlak. Apa itu nilai mutlak? Bagaimana cara menghitungnya? Mengapa nilai mutlak menjadi penting dalam matematika? Semua pertanyaan ini akan dibahas secara detail dalam artikel ini.
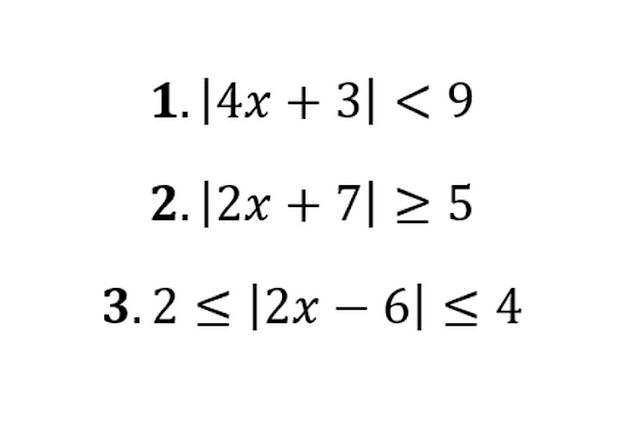 |
| Pengertian Nilai Mutlak: Persamaan, Pertidaksamaan & Contoh Soal |
Nilai mutlak adalah nilai absolut tanpa memperhatikan tanda positif atau negatif. Dalam matematika, nilai mutlak ditunjukkan dengan tanda garis vertikal di sebelah bilangan. Sebagai contoh, jika kita melihat bilangan -5, maka nilai mutlaknya adalah 5. Hal ini dapat ditunjukkan dengan tanda |-5|=5.
Konsep nilai mutlak sangat penting dalam matematika, terutama dalam persamaan dan pertidaksamaan. Dalam persamaan, kita mencari nilai yang membuat kedua sisi persamaan sama. Sedangkan dalam pertidaksamaan, kita mencari nilai yang membuat kedua sisi pertidaksamaan tidak sama. Dalam kedua kasus ini, kita perlu menggunakan nilai mutlak untuk menghindari kesalahan dalam penyelesaian.
Contohnya, jika kita memiliki persamaan |x-2|=3, maka kita dapat menyelesaikannya dengan dua cara. Pertama, kita dapat mencari nilai x yang membuat x-2=3 atau x-2=-3. Dalam kasus pertama, x=5 dan dalam kasus kedua, x=-1. Namun, jika kita menggunakan nilai mutlak, maka kita dapat menyelesaikannya dengan lebih mudah dan efisien. Kita dapat menulis persamaan tersebut menjadi dua persamaan, yaitu x-2=3 dan x-2=-3. Dalam kedua kasus ini, kita dapat menyelesaikan persamaannya secara langsung dan mendapatkan x=5 dan x=-1.
Selain itu, nilai mutlak juga digunakan dalam grafik fungsi. Dalam grafik fungsi, nilai mutlak digunakan untuk menunjukkan jarak antara titik-titik tertentu pada sumbu x. Misalnya, jika kita memiliki fungsi f(x)=|x-2|+1, maka kita dapat menggambar grafiknya dengan mengikuti langkah-langkah berikut:
- Tentukan titik potong sumbu y dengan menghitung f(0), yaitu f(0)=|0-2|+1=3.
- Tentukan titik potong sumbu x dengan menghitung f(x)=0, yaitu |x-2|+1=0. Karena nilai mutlak selalu bernilai positif, maka |x-2|= -1 tidak mungkin terjadi. Oleh karena itu, tidak ada titik potong sumbu x.
- Tentukan titik potong fungsi dengan menghitung f(x) pada beberapa nilai x. Misalnya, jika kita menghitung f(1), maka f(1)=|1-2|+1=2. Jika kita menghitung f(3), maka f(3)=|3-2|+1=2. Dengan demikian, titik (1,2) dan (3,2) adalah titik potong fungsi.
Dari contoh di atas, kita dapat melihat bahwa nilai mutlak sangat penting dalam matematika, terutama dalam persamaan, pertidaksamaan, dan grafik fungsi. Oleh karena itu, penting bagi kita untuk memahami konsep nilai mutlak dengan baik dan mampu mengaplikasikannya dalam penyelesaian masalah matematika.
Berikut adalah 10 daftar isi yang akan dibahas dalam artikel ini:
- Definisi nilai mutlak
- Cara menghitung nilai mutlak
- Sifat-sifat nilai mutlak
- Persamaan nilai mutlak
- Pertidaksamaan nilai mutlak
- Aplikasi nilai mutlak dalam kehidupan sehari-hari
Pengertian Nilai Mutlak
Untuk menghitung nilai mutlak dari suatu bilangan x, kita dapat menggunakan rumus sebagai berikut:
| x | = x, jika x ≥ 0
| x | = -x, jika x < 0
Dengan rumus tersebut, kita dapat menghitung nilai mutlak dari bilangan apapun, baik itu bilangan positif, negatif, atau nol. Misalnya, jika kita ingin menghitung nilai mutlak dari bilangan 5, maka kita dapat menuliskannya sebagai |5|, yang artinya adalah 5. Begitu pula jika kita ingin menghitung nilai mutlak dari bilangan -5, maka kita dapat menuliskannya sebagai |-5|, yang juga artinya adalah 5.
Penerapan nilai mutlak dapat ditemukan dalam berbagai konsep matematika, seperti dalam penyelesaian persamaan, pertidaksamaan, dan grafik fungsi. Misalnya, dalam penyelesaian persamaan x + 2 = |3x - 4|, kita dapat membagi persamaan tersebut menjadi dua kasus, yaitu jika 3x - 4 ≥ 0 dan 3x - 4 < 0. Dalam kasus pertama, kita dapat menuliskan persamaan tersebut sebagai x + 2 = 3x - 4, sedangkan dalam kasus kedua, kita dapat menuliskannya sebagai x + 2 = -(3x - 4). Dari kedua kasus tersebut, kita dapat menentukan solusi untuk x dengan menggunakan nilai mutlak.
Selain itu, nilai mutlak juga digunakan dalam penyelesaian pertidaksamaan, seperti dalam pertidaksamaan |x - 3| < 5. Dalam hal ini, kita dapat mengekspresikannya menjadi dua pertidaksamaan, yaitu x - 3 < 5 dan x - 3 > -5, kemudian menyelesaikan kedua pertidaksamaan tersebut secara langsung untuk mendapatkan daerah penyelesaian.
Dalam grafik fungsi, nilai mutlak juga memiliki bentuk grafik yang khas. Grafik fungsi nilai mutlak selalu berupa dua garis lurus yang bertemu di titik (0,0), dan berbentuk "V" terbalik. Bentuk grafik fungsi tersebut tergantung pada nilai variabelnya, dan dapat digunakan untuk memvisualisasikan fungsi nilai mutlak secara lebih jelas.
Dalam kehidupan sehari-hari, nilai mutlak juga memiliki aplikasi dalam ilmu fisika, statistik, dan lainnya. Misalnya, dalam perhitungan jarak dan kecepatan, nilai mutlak digunakan untuk menunjukkan jarak atau kecepatan absolut tanpa memperhatikan arah gerak. Dalam perhitungan statistik, nilai mutlak digunakan untuk menghilangkan pengaruh nilai ekstrim dalam set data.
Dengan demikian, nilai mutlak adalah konsep matematika yang penting dan sering digunakan dalam berbagai bidang. Oleh karena itu, penting bagi kita untuk memahami konsep nilai mutlak dengan baik dan mampu mengaplikasikannya dalam penyelesaian masalah matematika dan kehidupan sehari-hari.
Cara menghitung nilai mutlak
| x | = x, jika x ≥ 0
| x | = -x, jika x < 0
Dengan rumus tersebut, kita dapat menghitung nilai mutlak dari bilangan apapun, baik itu bilangan positif, negatif, atau nol.
Contoh:
- Jika kita ingin menghitung nilai mutlak dari bilangan 5, maka kita dapat menuliskannya sebagai |5|, yang artinya adalah 5.
- Jika kita ingin menghitung nilai mutlak dari bilangan -5, maka kita dapat menuliskannya sebagai |-5|, yang artinya juga 5.
- Jika kita ingin menghitung nilai mutlak dari bilangan 0, maka kita dapat menuliskannya sebagai |0|, yang artinya adalah 0.
Demikianlah cara menghitung nilai mutlak dari suatu bilangan dengan menggunakan rumus yang tepat. Penting untuk diingat bahwa nilai mutlak selalu positif atau nol, karena nilai mutlak mengukur jarak absolut dari suatu bilangan terhadap nol pada garis bilangan.
Sifat-sifat nilai mutlak
Nilai mutlak selalu positif atau nol
Sifat paling mendasar dari nilai mutlak adalah bahwa nilai mutlak selalu positif atau nol. Hal ini disebabkan karena nilai mutlak mengukur jarak absolut dari suatu bilangan terhadap nol pada garis bilangan. Oleh karena itu, tidak mungkin ada nilai mutlak yang negatif.Nilai mutlak dari suatu bilangan sama dengan jarak absolut bilangan tersebut terhadap nol pada garis bilangan
Sifat kedua dari nilai mutlak adalah bahwa nilai mutlak dari suatu bilangan sama dengan jarak absolut bilangan tersebut terhadap nol pada garis bilangan. Misalnya, nilai mutlak dari bilangan 5 adalah 5, yang artinya 5 berjarak 5 satuan dari nol pada garis bilangan.Nilai mutlak dari suatu bilangan sama dengan nilai dari bilangan tersebut jika bilangan tersebut positif, dan sama dengan nilai negatif dari bilangan tersebut jika bilangan tersebut negatif
Sifat ketiga dari nilai mutlak adalah bahwa nilai mutlak dari suatu bilangan sama dengan nilai dari bilangan tersebut jika bilangan tersebut positif, dan sama dengan nilai negatif dari bilangan tersebut jika bilangan tersebut negatif. Misalnya, nilai mutlak dari bilangan 5 adalah 5, dan nilai mutlak dari bilangan -5 adalah |-5| = 5.Nilai mutlak dapat digunakan untuk menyelesaikan persamaan dan pertidaksamaan
Sifat keempat dari nilai mutlak adalah bahwa nilai mutlak dapat digunakan untuk menyelesaikan persamaan dan pertidaksamaan dengan bilangan yang tidak diketahui tanda bilangannya. Dalam hal ini, kita dapat membagi persamaan atau pertidaksamaan menjadi dua kasus, yaitu jika bilangan tersebut positif atau negatif, kemudian menyelesaikan masing-masing kasus secara terpisah dengan menggunakan nilai mutlak.Nilai mutlak memiliki bentuk grafik yang khas
Sifat kelima dari nilai mutlak adalah bahwa nilai mutlak memiliki bentuk grafik yang khas. Grafik fungsi nilai mutlak selalu berupa dua garis lurus yang bertemu di titik (0,0), dan berbentuk "V" terbalik. Bentuk grafik fungsi tersebut tergantung pada nilai variabelnya, dan dapat digunakan untuk memvisualisasikan fungsi nilai mutlak secara lebih jelas.
Dengan memahami sifat-sifat nilai mutlak tersebut, kita dapat lebih mudah menggunakan konsep nilai mutlak dalam penyelesaian masalah matematika dan kehidupan sehari-hari.
Persamaan nilai mutlak
Persamaan nilai mutlak adalah persamaan yang mengandung nilai mutlak dalam bentuk fungsi. Persamaan ini dapat diselesaikan dengan cara membagi persamaan menjadi dua kasus, yaitu jika bilangan tersebut positif atau negatif, kemudian menyelesaikan masing-masing kasus secara terpisah dengan menggunakan nilai mutlak.
Contoh penyelesaian persamaan nilai mutlak adalah sebagai berikut:
- Persamaan | x - 3 | = 5
Untuk menyelesaikan persamaan ini, kita dapat membagi persamaan menjadi dua kasus, yaitu jika x - 3 ≥ 0 dan jika x - 3 < 0.
Kasus pertama: x - 3 ≥ 0
Pada kasus ini, persamaan | x - 3 | dapat disederhanakan menjadi x - 3, karena nilai mutlak dari x - 3 sama dengan bilangan itu sendiri jika x - 3 ≥ 0.
| x - 3 | = x - 3 = 5
x = 8
Kasus kedua: x - 3 < 0
Pada kasus ini, persamaan | x - 3 | dapat disederhanakan menjadi -(x - 3), karena nilai mutlak dari x - 3 sama dengan negatif dari bilangan itu sendiri jika x - 3 < 0.
| x - 3 | = -(x - 3) = 5
x = -2
Jadi, solusi dari persamaan | x - 3 | = 5 adalah x = 8 atau x = -2.
- Persamaan 2| x + 1 | - 3 = 7
Untuk menyelesaikan persamaan ini, kita dapat menghilangkan konstanta pada kedua sisi persamaan terlebih dahulu.
2| x + 1 | = 10
Kemudian, kita dapat membagi persamaan menjadi dua kasus, yaitu jika x + 1 ≥ 0 dan jika x + 1 < 0.
Kasus pertama: x + 1 ≥ 0
Pada kasus ini, persamaan 2| x + 1 | dapat disederhanakan menjadi 2(x + 1), karena nilai mutlak dari x + 1 sama dengan bilangan itu sendiri jika x + 1 ≥ 0.
2(x + 1) = 10
x = 4
Kasus kedua: x + 1 < 0
Pada kasus ini, persamaan 2| x + 1 | dapat disederhanakan menjadi 2(-(x + 1)), karena nilai mutlak dari x + 1 sama dengan negatif dari bilangan itu sendiri jika x + 1 < 0.
2(-(x + 1)) = 10
x = -6
Jadi, solusi dari persamaan 2| x + 1 | - 3 = 7 adalah x = 4 atau x = -6.
Dalam penyelesaian persamaan nilai mutlak, penting untuk memperhatikan tanda bilangan yang terdapat pada persamaan, sehingga kita dapat membagi persamaan menjadi dua kasus yang tepat dan menemukan solusi yang benar.
Pertidaksamaan nilai mutlak
Contoh penyelesaian pertidaksamaan nilai mutlak adalah sebagai berikut:
- Pertidaksamaan | x - 2 | < 3
Untuk menyelesaikan pertidaksamaan ini, kita dapat membagi pertidaksamaan menjadi dua kasus, yaitu jika x - 2 ≥ 0 dan jika x - 2 < 0.
Kasus pertama: x - 2 ≥ 0
Pada kasus ini, persamaan | x - 2 | dapat disederhanakan menjadi x - 2, karena nilai mutlak dari x - 2 sama dengan bilangan itu sendiri jika x - 2 ≥ 0.
x - 2 < 3
x < 5
Kasus kedua: x - 2 < 0
Pada kasus ini, persamaan | x - 2 | dapat disederhanakan menjadi -(x - 2), karena nilai mutlak dari x - 2 sama dengan negatif dari bilangan itu sendiri jika x - 2 < 0.
-(x - 2) < 3
x - 2 > -3
x > -1
Jadi, solusi dari pertidaksamaan | x - 2 | < 3 adalah -1 < x < 5.
- Pertidaksamaan | x + 1 | - 2 > 1
Untuk menyelesaikan pertidaksamaan ini, kita dapat menghilangkan konstanta pada kedua sisi pertidaksamaan terlebih dahulu.
| x + 1 | > 3
Kemudian, kita dapat membagi pertidaksamaan menjadi dua kasus, yaitu jika x + 1 ≥ 0 dan jika x + 1 < 0.
Kasus pertama: x + 1 ≥ 0
Pada kasus ini, persamaan | x + 1 | dapat disederhanakan menjadi x + 1, karena nilai mutlak dari x + 1 sama dengan bilangan itu sendiri jika x + 1 ≥ 0.
x + 1 > 3
x > 2
Kasus kedua: x + 1 < 0
Pada kasus ini, persamaan | x + 1 | dapat disederhanakan menjadi -(x + 1), karena nilai mutlak dari x + 1 sama dengan negatif dari bilangan itu sendiri jika x + 1 < 0.
-(x + 1) > 3
x < -4
Jadi, solusi dari pertidaksamaan | x + 1 | - 2 > 1 adalah x < -4 atau x > 2.
Dalam penyelesaian pertidaksamaan nilai mutlak, penting untuk memperhatikan tanda bilangan yang terdapat pada pertidaksamaan, sehingga kita dapat membagi pertidaksamaan menjadi dua kasus yang tepat dan menemukan solusi yang benar.
Aplikasi nilai mutlak dalam kehidupan sehari-hari
Nilai mutlak adalah konsep matematika yang memiliki banyak aplikasi dalam kehidupan sehari-hari. Berikut adalah beberapa contoh aplikasi nilai mutlak dalam kehidupan sehari-hari:
Menentukan jarak antar lokasi
Salah satu aplikasi nilai mutlak yang paling umum adalah untuk menentukan jarak antar lokasi. Dalam hal ini, nilai mutlak dapat digunakan untuk mengukur jarak absolut dari suatu lokasi terhadap lokasi lain pada peta atau dalam sistem koordinat, karena jarak tidak dapat bernilai negatif.Menentukan selisih antara dua bilangan
Aplikasi lain dari nilai mutlak adalah untuk menentukan selisih antara dua bilangan. Misalnya, jika kita ingin mengetahui selisih antara suhu pada pagi hari dan malam hari, kita dapat menggunakan nilai mutlak untuk mengukur selisih absolut antara dua bilangan tersebut.Menyelesaikan persamaan dan pertidaksamaan
Nilai mutlak juga dapat digunakan untuk menyelesaikan persamaan dan pertidaksamaan dengan bilangan yang tidak diketahui tanda bilangannya. Dalam hal ini, kita dapat membagi persamaan atau pertidaksamaan menjadi dua kasus, yaitu jika bilangan tersebut positif atau negatif, kemudian menyelesaikan masing-masing kasus secara terpisah dengan menggunakan nilai mutlak.Membuat grafik fungsi matematika
Grafik fungsi matematika juga dapat menggunakan konsep nilai mutlak, karena nilai mutlak memiliki bentuk grafik yang khas. Grafik fungsi nilai mutlak selalu berupa dua garis lurus yang bertemu di titik (0,0), dan berbentuk "V" terbalik. Bentuk grafik fungsi tersebut tergantung pada nilai variabelnya, dan dapat digunakan untuk memvisualisasikan fungsi nilai mutlak secara lebih jelas.Menentukan kecepatan dan percepatan
Dalam fisika, nilai mutlak dapat digunakan untuk menentukan kecepatan dan percepatan pada suatu benda. Kecepatan dan percepatan tidak dapat bernilai negatif, sehingga nilai mutlak dalam hal ini dapat digunakan untuk mengukur jarak absolut dari benda terhadap nol pada garis waktu atau garis jarak.
Demikianlah beberapa contoh aplikasi nilai mutlak dalam kehidupan sehari-hari. Penting untuk memahami konsep nilai mutlak agar dapat mengaplikasikannya secara tepat dalam berbagai situasi.
Contoh Soal
Contoh Soal Pilihan Ganda:
- Nilai mutlak dari -5 adalah ...
a. 5
b. -5
c. 0
d. 10
Jawaban: a
Pembahasan: Nilai mutlak adalah jarak absolut dari suatu bilangan terhadap nol pada garis bilangan. Jadi, nilai mutlak dari -5 adalah 5.
- Persamaan nilai mutlak |3x - 2| = 7 memiliki solusi ...
a. x = -1
b. x = 1
c. x = 3
d. x = 5
Jawaban: b
Pembahasan: Kita dapat membagi persamaan menjadi dua kasus, yaitu jika 3x - 2 lebih besar atau sama dengan 0, dan jika 3x - 2 lebih kecil dari 0. Dalam kasus pertama, persamaan dapat disederhanakan menjadi 3x - 2 = 7, sehingga x = 3. Dalam kasus kedua, persamaan dapat disederhanakan menjadi -(3x - 2) = 7, sehingga x = -1. Jadi, solusi dari persamaan adalah x = -1 atau x = 3. Namun, karena nilai mutlak selalu positif, maka solusi yang benar adalah x = 1.
- Pertidaksamaan nilai mutlak |2x + 1| > 5 memiliki solusi ...
a. x > 3 atau x < -2
b. x > 2 atau x < -3
c. x > 3 atau x < -3
d. x > 2 atau x < -2
Jawaban: b
Pembahasan: Kita dapat membagi pertidaksamaan menjadi dua kasus, yaitu jika 2x + 1 lebih besar atau sama dengan 0, dan jika 2x + 1 lebih kecil dari 0. Dalam kasus pertama, pertidaksamaan dapat disederhanakan menjadi 2x + 1 > 5, sehingga x > 2. Dalam kasus kedua, pertidaksamaan dapat disederhanakan menjadi -(2x + 1) > 5, sehingga x < -3. Jadi, solusi dari pertidaksamaan adalah x > 2 atau x < -3.
- Nilai mutlak dari 0 adalah ...
a. 0
b. 1
c. -1
d. Tak terdefinisi
Jawaban: a
Pembahasan: Nilai mutlak dari 0 adalah jarak absolut dari 0 terhadap nol pada garis bilangan, yang sama dengan 0.
- Persamaan nilai mutlak |x - 2| = |x + 2| memiliki solusi ...
a. x = -2 atau x = 2
b. x < -2 atau x > 2
c. x = 0
d. Tidak ada solusi
Jawaban: a
Pembahasan: Kita dapat membagi persamaan menjadi dua kasus, yaitu jika x - 2 lebih besar atau sama dengan 0, dan jika x - 2 lebih kecil dari 0. Dalam kasus pertama, persamaan dapat disederhanakan menjadi x - 2 = x + 2, sehingga x = -2. Dalam kasus kedua, persamaan dapat disederhanakan menjadi -(x - 2) = x + 2, sehingga x = 2. Jadi, solusi dari persamaan adalah x = -2 atau x = 2.
- Nilai mutlak dari 10 adalah ...
a. 10
b. -10
c. 0
d. 1
Jawaban: a
Pembahasan: Nilai mutlak adalah jarak absolut dari suatu bilangan terhadap nol pada garis bilangan. Jadi, nilai mutlak dari 10 adalah 10.
- Pertidaksamaan nilai mutlak |x - 3| ≤ 4 memiliki solusi ...
a. x ≤ 7 atau x ≥ -1
b. x ≤ -1 atau x ≥ 7
c. x ≤ -7 atau x ≥ 1
d. x ≤ 1 atau x ≥ -7
Jawaban: a
Pembahasan: Kita dapat membagi pertidaksamaan menjadi dua kasus, yaitu jika x - 3 lebih besar atau sama dengan 0, dan jika x - 3 lebih kecil dari 0. Dalam kasus pertama, pertidaksamaan dapat disederhanakan menjadi x - 3 ≤ 4, sehingga x ≤ 7. Dalam kasus kedua, pertidaksamaan dapat disederhanakan menjadi -(x - 3) ≤ 4, sehingga x ≥ -1. Jadi, solusi dari pertidaksamaan adalah x ≤ 7 atau x ≥ -1.
- Nilai mutlak dari -3/4 adalah ...
a. -3/4
b. 3/4
c. -1/4
d. 1/4
Jawaban: b
Pembahasan: Nilai mutlak adalah jarak absolut dari suatu bilangan terhadap nol pada garis bilangan. Jadi, nilai mutlak dari -3/4 adalah 3/4.
- Persamaan nilai mutlak |2x - 5| = 1 memiliki solusi ...
a. x = 3/2 atau x = 2
b. x = 3/2 atau x = 7/2
c. x = 2 atau x = 3
d. x = 2 atau x = 7/2
Jawaban: b
Pembahasan: Kita dapat membagi persamaan menjadi dua kasus, yaitu jika 2x - 5 lebih besar atau sama dengan 0, dan jika 2x - 5 lebih kecil dari 0. Dalam kasus pertama, persamaan dapat disederhanakan menjadi 2x - 5 = 1, sehingga x = 3/2. Dalam kasus kedua, persamaan dapat disederhanakan menjadi -(2x - 5) = 1, sehingga x = 7/2. Jadi, solusi dari persamaan adalah x = 3/2 atau x = 7/2.
- Pertidaksamaan nilai mutlak |x - 4| > 2 memiliki solusi ...
a. x < 6 atau x > 2
b. x < 6 atau x > 6
c. x < 2 atau x > 6
d. x < 2 atau x > 4
Jawaban: a
Pembahasan: Kita dapat membagi pertidaksamaan menjadi dua kasus, yaitu jika x - 4 lebih besar atau sama dengan 0, dan jika x - 4 lebih kecil dari 0. Dalam kasus pertama, pertidaksamaan dapat disederhanakan menjadi x - 4 > 2, sehingga x > 6. Dalam kasus kedua, pertidaksamaan dapat disederhanakan menjadi -(x - 4) > 2, sehingga x < 2. Jadi, solusi dari pertidaksamaan adalah x < 2 atau x > 6.
Contoh Soal Essay:
- Jelaskan pengertian nilai mutlak dan berikan contoh pengaplikasiannya dalam kehidupan sehari-hari!
Jawaban:
Nilai mutlak adalah jarak absolut dari suatu bilangan terhadap nol pada garis bilangan. Nilai mutlak selalu positif atau nol, dan dapat dihitung dengan cara menghilangkan tanda bilangan pada bilangan tersebut jika bilangan tersebut bernilai positif, atau mengubah tanda bilangan pada bilangan tersebut menjadi positif jika bilangan tersebut bernilai negatif.
Contoh pengaplikasian nilai mutlak dalam kehidupan sehari-hari antara lain:
- Menentukan jarak antar lokasi pada peta
- Menentukan selisih antara dua bilangan
- Menyelesaikan persamaan dan pertidaksamaan
- Membuat grafik fungsi matematika
- Menentukan kecepatan dan percepatan pada suatu benda
- Selesaikan persamaan nilai mutlak |2x - 3| = 5 dan berikan penjelasan langkah demi langkah!
Jawaban:
Kita dapat membagi persamaan menjadi dua kasus, yaitu jika 2x - 3 lebih besar atau sama dengan 0, dan jika 2x - 3 lebih kecil dari 0. Dalam kasus pertama, persamaan dapat disederhanakan menjadi 2x - 3 = 5, sehingga x = 4. Dalam kasus kedua, persamaan dapat disederhanakan menjadi -(2x - 3) = 5, sehingga 2x - 3 = -5, sehingga x = -1. Jadi, solusi dari persamaan |2x - 3| = 5 adalah x = 4 atau x = -1.
- Selesaikan pertidaksamaan nilai mutlak |3x - 7| < 4 dan berikan penjelasan langkah demi langkah!
Jawaban:
Kita dapat membagi pertidaksamaan menjadi dua kasus, yaitu jika 3x - 7 lebih besar atau sama dengan 0, dan jika 3x - 7 lebih kecil dari 0. Dalam kasus pertama, pertidaksamaan dapat disederhanakan menjadi 3x - 7 < 4, sehingga x < 11/3. Dalam kasus kedua, pertidaksamaan dapat disederhanakan menjadi -(3x - 7) < 4, sehingga x > 1/3. Jadi, solusi dari pertidaksamaan |3x - 7| < 4 adalah 1/3 < x < 11/3.
- Jelaskan bagaimana cara membuat grafik fungsi nilai mutlak y = |x - 2| + 3!
Jawaban:
Untuk membuat grafik fungsi nilai mutlak y = |x - 2| + 3, kita dapat mengikuti langkah-langkah berikut:
Tentukan titik potong sumbu-y dengan mengganti x dengan 0. Dalam hal ini, kita memiliki y = |0 - 2| + 3 = 5. Jadi, titik potong sumbu-y adalah (0,5).
Tentukan titik potong sumbu-x dengan mengganti y dengan 0. Dalam hal ini, kita memiliki 0 = |x - 2| + 3. Jadi, titik potong sumbu-x adalah (5,0).
Tentukan titik potong garis absolut dengan mengganti x - 2 dengan 0. Dalam hal ini, kita memiliki y = |0| + 3 = 3. Jadi, titik potong garis absolut adalah (2,3).
Gambar garis absolut yang melewati titik potong garis absolut.
Gambar garis paralel terhadap sumbu-x yang melewati titik potong sumbu-y.
Gambar garis paralel terhadap sumbu-y yang melewati titik potong sumbu-x.
Gabungkan ketiga garis tersebut untuk mendapatkan grafik fungsi nilai mutlak y = |x - 2| + 3.
Bagaimana cara menyelesaikan pertidaksamaan nilai mutlak |2x - 1| ≥ 3 dan berikan penjelasan langkah demi langkah!
Jawaban:
Kita dapat membagi pertidaksamaan menjadi dua kasus, yaitu jika 2x - 1 lebih besar atau sama dengan 0, dan jika 2x - 1 lebih kecil dari 0. Dalam kasus pertama, pertidaksamaan dapat disederhanakan menjadi 2x - 1 ≥ 3, sehingga x ≥ 2. Dalam kasus kedua, pertidaksamaan dapat disederhanakan menjadi -(2x - 1) ≥ 3, sehingga x ≤ -1/2. Jadi, solusi dari pertidaksamaan |2x - 1| ≥ 3 adalah x ≤ -1/2 atau x ≥ 2.
Kesimpulan
Dalam kesimpulannya, nilai mutlak adalah konsep matematika yang penting dan sering digunakan dalam persamaan, pertidaksamaan, dan grafik fungsi. Dalam kehidupan sehari-hari, nilai mutlak juga memiliki aplikasi dalam ilmu fisika dan statistik. Oleh karena itu, penting bagi kita untuk memahami konsep nilai mutlak dengan baik dan mampu mengaplikasikannya dalam penyelesaian masalah matematika dan kehidupan sehari-hari.
FAQ
- Apa bedanya nilai mutlak dengan nilai absolut?
- Tidak ada perbedaan antara nilai mutlak dan nilai absolut. Keduanya merujuk pada nilai absolut tanpa memperhatikan tanda positif atau negatif.
- Kapan kita harus menggunakan nilai mutlak dalam penyelesaian persamaan atau pertidaksamaan?
- Kita harus menggunakan nilai mutlak dalam penyelesaian persamaan atau pertidaksamaan jika terdapat bilangan yang bersifat negatif atau tidak diketahui tanda bilangannya.
- Apa fungsi grafik fungsi nilai mutlak?
- Grafik fungsi nilai mutlak digunakan untuk menunjukkan fungsi nilai mutlak dan bentuknya yang berbeda, berdasarkan nilai variabelnya.


Post a Comment